数组
数组是用于储存多个相同类型数据的集合,使用一段连续的内存空间存储数据
数组作为最基本的数据结构,想必大家一定已经足够了解,数组的增删操作时间复杂度是O(n),而查询的时间复杂度是O(1),这里的查询指的是按下标进行查找,如果是比对数据进行查询时间复杂度还是O(n)
前提:
假设数组的长度是n
新增操作:
我们新增一条数据到数组中时,当新增的数据在末尾的时候时间复杂度是O(1),而当新增的数据插入到数组的第x个位置时,由于数组使用的是连续的内存,所以x之后的数据都需要往后移动一位,把第x位置腾出来,才可以将新增的数据插入到第x个位置,如果按最坏的情况考虑,是将数据插入到数据的首位,这时数组里所有的数据都需要往后移一位,这时的时间复杂度就是O(n),所以平均的时间复杂度就是O(n)
删除操作:
当我们从数组中删除一条数据的时候,假设删除的数据位于数组的第x位置,也是由于数组使用的是连续的内存,当我们把x位置的数据删除之后,为了保证数组的内存是连续的,x位置之后的数据都需要往前移动一位,假设当删除的是数组首位的数据,这时首位之后的所有数据都需要往前移动一位,时间复杂度是O(n),当删除的数据是数组尾部的数据时,不会发生数据移动,时间复杂度是O(1)
查询操作:
关于查询,要说的点还是,由于数组的内存是连续的,这就提供了我们随机访问的能力,随机访问的意思就是指我们可以按照数组的下标进行查询,这时的时间复杂度是O(1),而遍历所有数组匹配查询的时候时间复杂度是O(n)
我们看一下数组在内存中的存储结构
//实例化一个数组,
int[] m = new int[]{0,5,10,15,20};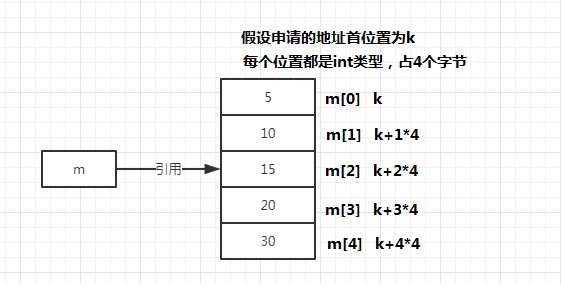
随机访问:由于数组内的地址是连续的,想要获取m[3]位置数据的时候我们只要根据寻址公式计算出m[3]的内存地址就可以直接获取到数据,这时假设数组的首地址是k,一个int类型占4个字节,m[3]的内存地址就是k+3*4
匹配查询:这时候由于需要遍历数组,如果在第一个m[0]的位置就匹配上,则时间复杂度是O(1),在数组尾位匹配上就是O(n),所以平均的时间复杂度就是O(n)
由于数组的容量是实例化的时候就固定的,所以没有办法进行动态扩容,而java中的容器类则弥补了这一缺陷,比如ArrayList,ArrayList将底层操作数组的细节封装,通过提供api供开发人员使用,ArrayList当我们调用add方法的时候不需要关心底层数组的容量够不够使用也不用关心扩容的逻辑是什么,当需要的扩容的时候ArrayList会自己进行扩容:
int newCapacity = oldCapacity + (oldCapacity >> 1);oldCapacity是数组的旧的容量大小,而newCapacity新的数组容量大小是原来的1.5倍(oldCapacity >> 1右移一位相当于oldCapacity/2)
扩容的原理就是计算出新的数组大小,然后申请内存,将原来的数组复制到新申请的数组中,这一过程是比较低效的,所以一般在实例化集合的时候都会指定集合的大小比如new ArrayList(16);
集合与数组对比:因为集合使用起来更方便,但数组也不是绝对不用,Java中的集合不支持基本类型,而这时候使用如果使用集合的话必然会进行装箱,拆箱的操作,造成不必要的性能消耗,所以当数据的容量是固定的,且数据类型是基本类型的时候,就可以考虑使用数组
总结:
由于数组存储的是相同类型的数据,并且内存的地址是连续的,就导致可以使用寻址公式计算出数组中某个元素的内存地址,所以数组的随机访问是高效的,但是要新增和删除数据的时候,为了保持数组的内存连续性,必然会导致数据的移动,所以数组的新增和删除是低效的
注意:使用数组需要警惕别造成数组越界
算法题
算法题来自leetcode
两数之和
链接:https://leetcode-cn.com/problems/two-sum/
难度:简单
给定一个整数数组 nums 和一个目标值 target,请你在该数组中找出和为目标值的那 两个 整数,并返回他们的数组下标。
你可以假设每种输入只会对应一个答案。但是,你不能重复利用这个数组中同样的元素。
示例:
给定 nums = [2, 7, 11, 15], target = 9
因为 nums[0] + nums[1] = 2 + 7 = 9
所以返回 [0, 1]思路:
nums[i]=target-nums[j]
题解:
class Solution {
public int[] twoSum(int[] nums, int target) {
Map<Integer,Integer> map = new HashMap<>(16);
for(int i=0;i<nums.length;i++){
int n = target-nums[i];
if(map.containsKey(target-nums[i])){
return new int[]{i,map.get(target-nums[i])};
}
map.put(nums[i],i);
}
return null;
}
}盛最多水的容器
链接:https://leetcode-cn.com/problems/container-with-most-water
难度:中等
给定 n 个非负整数 a1,a2,…,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明:你不能倾斜容器,且 n 的值至少为 2。
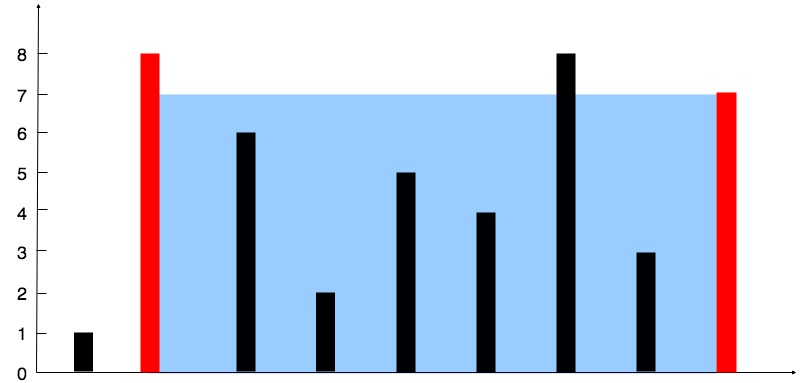
图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49
示例:
输入: [1,8,6,2,5,4,8,3,7]
输出: 49思路:
官方题解:双指针法
面积=长度(x)*高度(y)
假设left为x轴左起点,right为x轴右起点,left对应的y轴高度为a[left],right对应的y轴高度为a[right],计算面积中的高度只能取a[left]和a[right]中小的那个,而长度的计算方式是right-left
,当a[left]>a[right]时,对应的x轴right就往前移动一位,反之left就往后移动一位
题解:
class Solution {
public int maxArea(int[] height) {
//x轴左起始位置
int left=0;
//x轴右起始位置
int right= height.length-1;
int maxarea = 0;
while(left<right){
//每次都需要计算面积,将面积更大的赋值给maxarea
maxarea = Math.max(maxarea,Math.min(height[left],height[right])*(right-left));
//如果左面的垂直线大于右面的垂直线
if(height[left]>height[right]){
//右面的往前移动一位
right--;
}else{
//左面的往后移动一位
left++;
}
}
return maxarea;
}
}接雨水
链接:https://leetcode-cn.com/problems/trapping-rain-water
难度:困难
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。

上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。 感谢 Marcos 贡献此图。
示例:
输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6思路:
解题思路也是使用双指针,没有思路的可详细看下官方题解双指针方法的那个动图
题解:
class Solution {
public int trap(int[] height) {
int left=0;
int right=height.length-1;
int maxLeft=0;
int maxRight=0;
int area =0;
while(left<right){
if(height[left]<height[right]){
if(height[left]>=maxLeft){
maxLeft = height[left];
}else{
area += maxLeft-height[left];
}
++left;
}else{
if(height[right]>=maxRight){
maxRight = height[right];
}else{
area += maxRight-height[right];
}
--right;
}
}
return area;
}
}参考:
极客时间:数据结构与算法之美
leetCode官网:https://leetcode-cn.com/problemset/all/